Löse Kakuro Rätsel

In diesem Leitfaden bieten wir eine Reihe praktischer Tipps zum Lösen von Kakuro-Puzzles, mit Schwierigkeiten, die vom Anfänger bis zum Experten reichen.

Um die Regeln zusammenzufassen: Kakuro ist ein Puzzlespiel auf einem kreuzwortähnlichen Brett, auf dem Ziffern verwendet werden, um sie zu den in den Definitionsquadraten des Brettes angegebenen Werten zusammenzufassen. Darüber hinaus kann innerhalb jeder Summengruppe jede Ziffer höchstens einmal erscheinen.

Die traditionelle Art, ein Kakuro-Rätsel zu lösen, ist inkrementell: Indem Sie die vorhandenen Informationen auf dem Brett verwenden, können Sie mit Sicherheit den Wert einer bestimmten Zelle finden, die nur einen möglichen Wert annehmen kann. Dann wird dieser Wert gefüllt und der Prozess wird wiederholt, bis alle Board-Zellen entdeckt wurden.

In einigen Situationen gibt es keine bestimmte Boardzelle, die nur eine Möglichkeit hat. In diesen Fällen muss jede der Möglichkeiten allein erforscht und durch Widersprüche beseitigt werden, bis nur noch eine Vorgehensweise besteht.

Wir stellten unten mehrere Methoden vor, um Fortschritte bei der Lösung des eigentlichen Rätsels zu erzielen.

Eindeutige Summen für spezifische Definitionen

Es gibt einige Definitionen, die nur auf eine bestimmte Art gelöst werden können:

• Die Summe 3 (über zwei Zellen) wird immer 1 +2 sein.
• Die Summe 4 (über zwei Zellen) wird immer 1 + 3 sein.
• Die Summe 17 (über zwei Zellen) wird immer 8 + 9 betragen.
• Die Summe 6 (über drei Zellen) wird immer 1 +2 + 3 sein.
• Die Summe 24 (über drei Zellen) wird immer 7+8 +9 betragen.

und so weiter... Normalerweise können Sie mit der Maus auf ein Kakuro-Raster über die Definitionsnummer fahren, und es wird ein Tooltip angezeigt, der alle Möglichkeiten enthält, diese Summe mit eindeutigen Ziffern in der Anzahl der verfügbaren Zellen zu schreiben.

Die Summen, die auf einzigartige Weise geschrieben werden können, sind in der Regel niedrige oder hohe Summen, die in der Antwort niedrige/hohe Ziffern erzwingen, um sie zu erreichen.

Eine einzigartige Schreibweise der Summe hilft, aber denken Sie daran, dass alle Permutationen gültig sind und Sie immer noch herausfinden müssen, welche tatsächliche Permutation auf der Tafel verwendet werden soll.

Zeilen/ Spalten-Beschrän

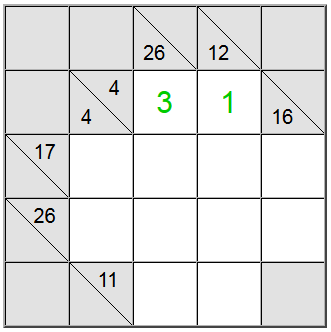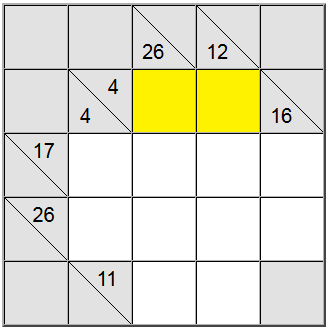
Für die oben hervorgehobenen gelben Zellen gibt es nur eine Möglichkeit, die Summe zu schreiben: 4 = 1 + 3. Wir müssen jedoch noch herausfinden, welche Permutation (1 + 3 oder 3 + 1) verwendet werden soll.

Es stellt sich heraus, dass uns die vertikale Definition von 26 hilft: Eine Summe von 4 Zellen, die die Ziffer 1 enthalten würde, wäre höchstens 1 + 9 + 8 = 7 = 25. Da unsere Summe 26 ist, stellt sich heraus, dass die Ziffer 1 kein Teil der Summe sein kann. Daher ist die einzige verbleibende Reihenfolge für die gelben Quadrate 3+1.

Schnittpunkte der Definitionen

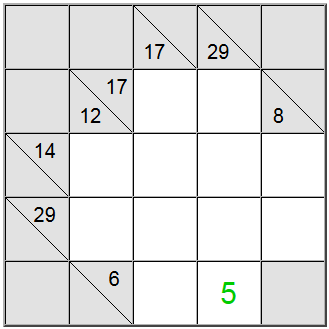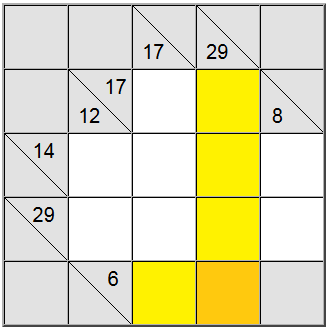
Auf der Tafel oben können die horizontalen gelben Quadrate als 6 = 1 + 5 oder 6 = 2 + 4 geschrieben werden. Die vertikale gelbe Summe kann nur als 29 = 5 + 7 + 8 + 9 geschrieben werden.

Das gelbe Quadrat, das am Schnittpunkt dieser beiden Summendefinitionen gefunden wird, muss dieselbe Ziffer enthalten, daher muss in den horizontalen und vertikalen Definitionen eine gemeinsame Ziffer vorhanden sein, um zwischen ihnen geteilt zu werden. Wenn wir uns die oben genannten Möglichkeiten ansehen, können wir leicht herausfinden, dass 5 die einzige Ziffer ist, die dieses Kriterium erfüllt.

Diese Technik funktioniert besonders gut, wenn eine Niedrigsumme mit einer Hochsummendefinition überschneidet wird. Niedrigsummen- und Hochsummendefinitionen sind diejenigen, die im Vergleich zur Anzahl der verfügbaren Zellen eine relativ niedrige oder hohe Summendefinitionsnummer (6 bzw. 29 für unser Beispiel) aufweisen. Da 6 relativ niedrig ist, erzwingt es niedrige Ziffern in der Summendarstellung und 29 erzwingen hohe Ziffern (um diese Summen unter Verwendung der angegebenen Anzahl von Zellen zu erreichen). Daher wird der Schnittpunkt von niedrigen und hohen Ziffern wahrscheinlich nur einen Kandidaten für den tatsächlichen Zellenwert enthalten.

Min/max Werte für eine Summengruppe

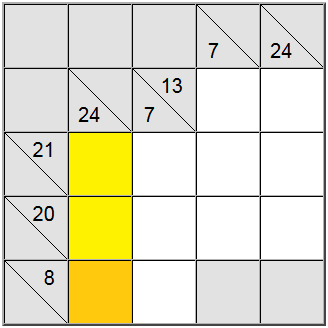
Manchmal ist es nützlich, den maximalen oder minimalen Wert für eine Summengruppe herauszufinden. Dies kann Ihnen ein Gefühl dafür vermitteln, was der gültige Ziffernbereich für diese bestimmte Summe ist, was Ihnen wiederum hilft, eine Korrelation mit anderen Einschränkungen herzustellen und die eindeutigen Aufgaben auf der Tafel zu ermitteln.

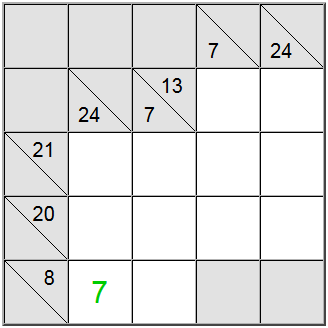
Im obigen Beispiel akzeptieren die gelben vertikalen Zellen nur Werte, die 7 oder höher sind. Wenn Sie versuchen, eine 6 zuzuweisen, können Sie leicht herausfinden, dass 6 + 9 und 8 = 23 ist, damit die Definitionssumme von 24 nicht erreichbar ist.

Da 7 ein Minimum ist, zwingt die horizontale Definition mit 8 als Summe die 7 in dieser Position.

Schlussfolgerung

Üben ist der beste Weg, um zu sehen, wie dieser Rat in tatsächlichen Kakuro-Spielen angewendet werden kann. Spiele ein Rätsel für Echt. Wir wünschen dir viel Glück und viel Spaß!

Spiel Kakuro